I. Principes de l'analyse différentielle
II. Implémentation
III. Exemples de représentations
IV. Intérêt pour la théorie musicale
V. Application à l'analyse de la musique électroacoustique
VI. Application à l'analyse de l'interprétation
VII. Conclusion et perspectives
Jean-Marc Chouvel (Université de Reims - CRLM - IDEAT UMR8153)
Jean Bresson (Ircam-CNRS UMR 9912)
Carlos Agon (Ircam-CNRS UMR 9912)
Mais la dualité
statique/dynamique de la représentation n'est pas seulement
valable pour la réduction symbolique de la partition. On peut la
retrouver aussi dans la représentation du signal. On peut
convertir la série précédente en forme d'onde
à partir du fichier MIDI correspondant dans un logiciel de
séquence. (on a utilisé ici Digital Performer et un
module de son externe Korg 05RW. Le son choisi est
désigné
par le terme "violon")
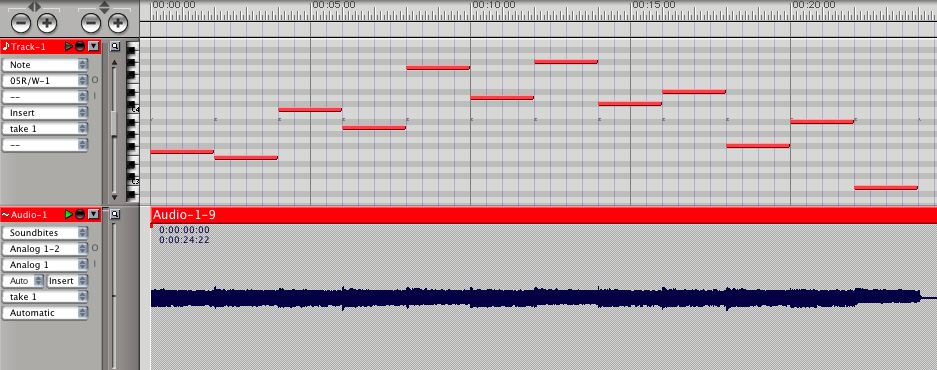
Fig. 2 : Conversion MIDI->Audio dans Digital Performer
< >

Fig. 2 : Conversion MIDI->Audio dans Digital Performer
La forme d'onde trahit à
peine la transition entre les notes et montre surtout
l'uniformité de la dynamique. La transformée de Fourier
réplique avec les harmoniques la logique déjà
visible dans le "piano roll" de la représentation MIDI. Comment
peut-on donner à cette représentation de la
répartition de l'énergie dans les bandes de
fréquences un sens "dynamique" ? Tout simplement en
représentant non pas l'énergie présente, mais la
diminution (valeurs négatives qui seront
représentées en bleu) ou l'augmentation (valeurs
positives représentées en rouge) d'énergie, soit
la différence entre l'état présent et
l'état antérieur, pour chaque bande de fréquence.
Si l'énergie se maintient identiquement, la Transformée
de Fourier Différentielle (TFD) sera nulle, que le signal soit
du silence ou un son assourdissant.
La figure 3 propose de visualiser la TFD de l'exemple précédent en alternance avec la Transformée de Fourier normale :
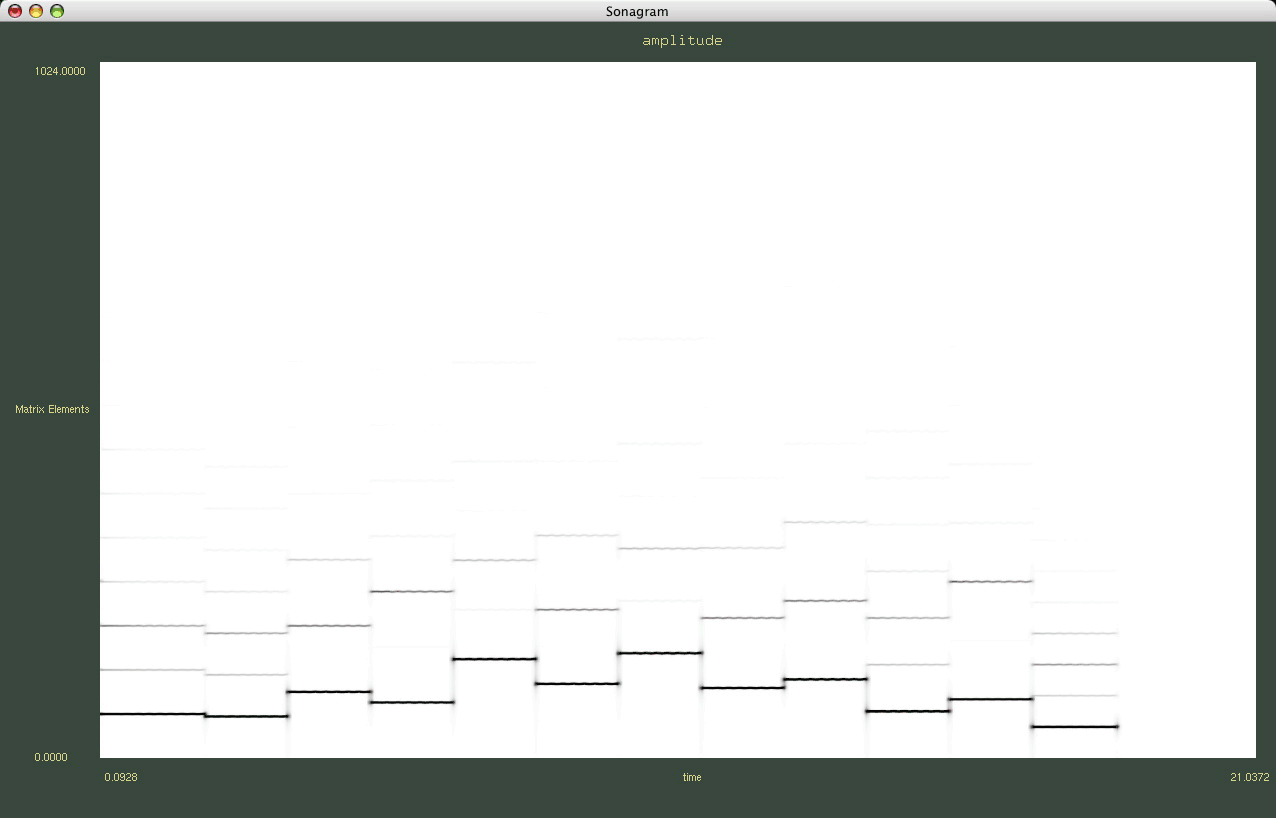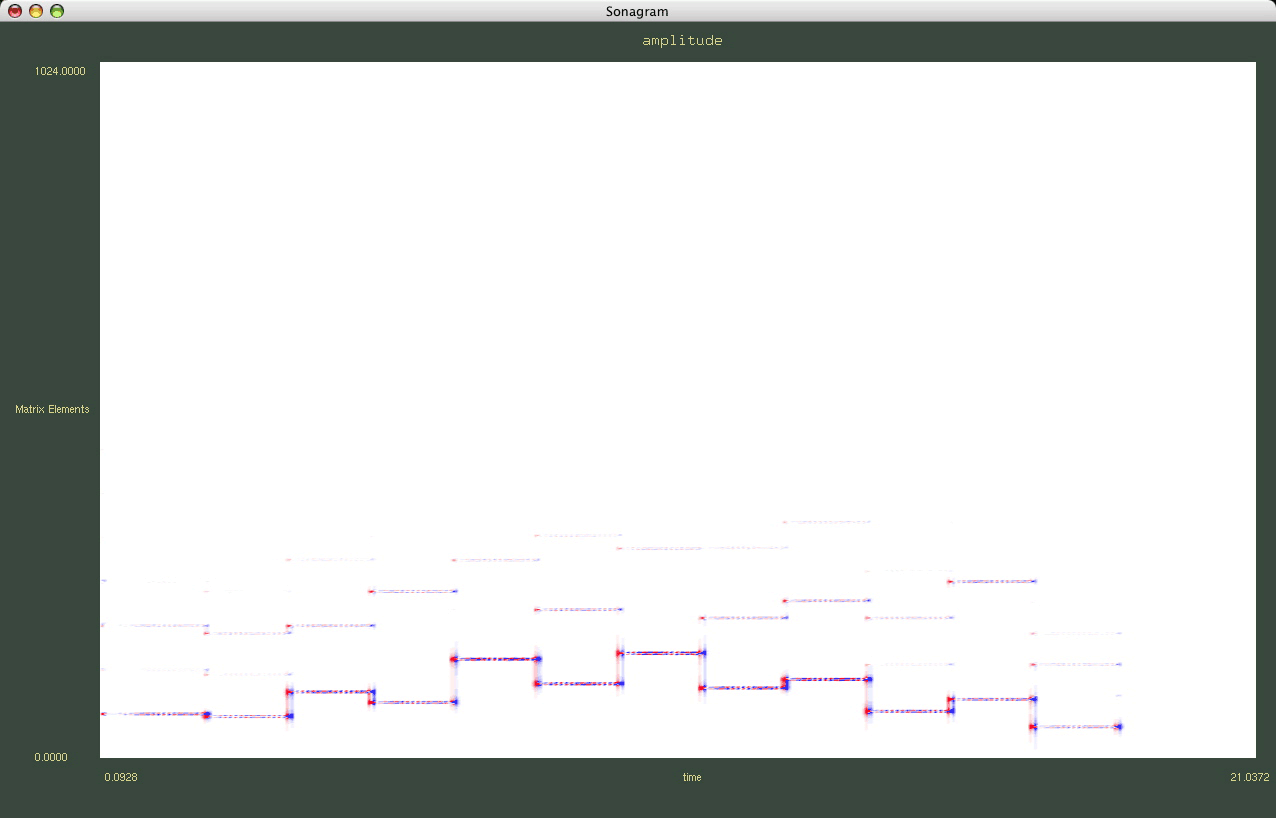
La figure 3 propose de visualiser la TFD de l'exemple précédent en alternance avec la Transformée de Fourier normale :

< >